Hilbert transform of complex signal
The Hilbert transform is important in signal processing, where it is a component of the analytic representation of a real-valued signal u(t). The Hilbert transform was first introduced by David Hilbert in this setting, to solve a special case of the Riemann–Hilbert problem for analytic functions. See more In mathematics and signal processing, the Hilbert transform is a specific singular integral that takes a function, u(t) of a real variable and produces another function of a real variable H(u)(t). The Hilbert transform is given … See more The Hilbert transform is a multiplier operator. The multiplier of H is σH(ω) = −i sgn(ω), where sgn is the signum function. Therefore: where See more In the following table, the frequency parameter $${\displaystyle \omega }$$ is real. Notes 1. ^ Some authors (e.g., Bracewell) use our −H as their definition of the forward transform. A … See more The Hilbert transform of u can be thought of as the convolution of u(t) with the function h(t) = 1/ π t, known as the Cauchy kernel. … See more The Hilbert transform arose in Hilbert's 1905 work on a problem Riemann posed concerning analytic functions, which has come to be known as the Riemann–Hilbert problem. Hilbert's work was mainly concerned with the Hilbert transform for functions defined on … See more It is by no means obvious that the Hilbert transform is well-defined at all, as the improper integral defining it must converge in a suitable sense. However, the Hilbert transform is … See more Boundedness If 1 < p < ∞, then the Hilbert transform on $${\displaystyle L^{p}(\mathbb {R} )}$$ is a bounded linear operator, meaning that there exists a constant Cp such that for all $${\displaystyle u\in L^{p}(\mathbb {R} )}$$ See more WebIn the paper, an accuracy of the discrete Hilbert transform method in a detection of amplitude and frequency of vibration signals has been examined. This issue was studied …
Hilbert transform of complex signal
Did you know?
WebMay 26, 2024 · The complex trace attributes are derived from the analytic signal. The most commonly used attributes are the envelope or reflection strength, the instantaneous … WebDie Hilbert-Transformation ist in der Funktionalanalysis, einem Teilgebiet der Mathematik, eine lineare Integraltransformation.Sie ist nach David Hilbert benannt, welcher sie Anfang des 20. Jahrhunderts bei Arbeiten am Riemann-Hilbert-Problem für holomorphe Funktionen formulierte. Erstmals explizit benannt wurde sie 1924 von Hardy basierend auf Arbeiten …
WebApr 20, 2024 · It is interesting to note that Hilbert transform [4] can be used to find a companion function (imaginary part in the equation above) to a real-valued signal such that the real signal can be analytically extended … WebFeb 16, 2016 · The Hilbert transform is a linear operator that produces a 90° phase shift in a signal, and it is a good first step in our exploration of phase. It is also commonly used in …
WebHilbert Transform, Analytic Signal and the Complex Envelope In Digital Signal Processing we often need to look at relationships between real and imaginary parts of a complex … WebFeb 1, 1991 · Introduction Hilbert transform relates the real and imaginary parts of the Fourier transform X (o~) of a causal sequence x (n). It also relates the log-magnitude and …
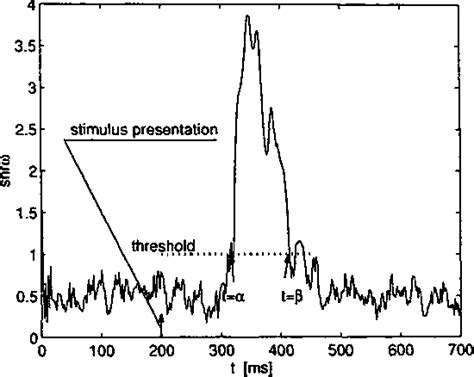
WebThe Hilbert transform of real-valued measured ERF is an analytic complex signal, represented by phase and amplitude. The temporal behaviour of the derivative of the phase, i.e. the instantaneous frequency, allows to distinguish time intervals containing meaningful signal from noise.
WebIn other words, the negative half of the frequency spectrum is zeroed out, turning the real-valued signal into a complex signal. The Hilbert transformed signal can be obtained from … ipkbl-sc motherboard manualWebmethods that call for two wavelet transforms, where one wavelet is (approximately) the Hilbert transform of the other. For example, Abry and Flandrin suggested it for transient detection [2] and turbulence analysis [1], Kingsbury suggested it for the complex dual-tree discrete wavelet transform (DWT) ipkd webshopWebResearching (High Level Discipline Journal Cluster English Platform), previously known as CLP Publishing (the English version of Chinese Optics Journal, 2024) was launched in April, 2024, which provides the platform for publishing world-class journals independently... orangeville family foot careWebJun 19, 2024 · Li et al. used the Hilbert transform to extract TOF features, albeit with a low location accuracy. ... In addition, the complex Morlet wavelet is a cosine signal that decays exponentially on both the left and right sides, and is similar to the freely attenuated Lamb wave signal waveform of the insulation structure; this method can achieve ... orangeville fencingWebIn mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. The real and imaginary parts of an analytic signal … ipkbl-vm motherboardWebhilbert returns a complex helical sequence, sometimes called the analytic signal, from a real data sequence. The analytic signal x = x r + j x i has a real part, x r , which is the original … ipke cornilsWebApr 16, 2024 · The Hilbert transform, defined by David Hilbert and named after him in 1924, was first discussed by G. H. Hardy mathematically. This transform arose while Hilbert was working on a problem called Riemann–Hilbert problem in 1905. Hilbert’s earlier work on discrete Hilbert transform was published in Hermann Weyl’s dissertation. orangeville family medical centre fax